레드 블랙 트리(Red Black Tree)는 이진 검색 트리의 한 종류이다. 이진 검색 트리가 무엇인지는 아래 문단에서 간단하게만 정리해두었으나, 이진검색트리의 순회나 노드의 삽입, 삭제 과정등을 전혀 모른다면 이진 검색트리를 먼저 공부한 후 레드 블랙트리를 공부하는 게 더 좋은 공부 순서일 것 같다!
💡 이진 검색 트리
이진트리의 한 종류. 각 노드들은 key, 부모 노드(p), 왼쪽 자식노드(left), 오른쪽 자식노드(right) 필드를 가지고 있고, 부모나 자식 노드가 없는 경우 각 필드는 NIL*값을 가진다. 부모가 없는 루트노드는 부모가 NIL인 유일한 노드이다. (*NIL이란 아무것도 없음을 뜻한다)
이진트리와 이진 검색 트리의 차이점은 모든 노드에서 왼쪽 자식은 부모노드보다 작거나 같고, 오른쪽 자식은 부모노드보다 크거나 같다는 특징을 가진다는 것이다. CLRS에서는 이를 "x를 이진 검색 트리의 한 노드라고 하자. y가 x의 왼쪽 서브트리의 한 노드면 y.key <= x.key를 만족한다. 그리고 y가 x의 오른쪽 서브트리의 한 노드면 y.key>= x.key를 만족한다" 와 같이 표현한다.
이진 검색 트리의 장점은 O(logN)이라는 시간복잡도로 빠른 검색이 가능하다는 것인데, 문제는 트리의 높이가 큰 경우(= 트리가 한 쪽으로 치우친 경우)에는 탐색의 시간복잡도가 O(N)에 가까워진다. 다른 말로 표현하면 트리의 높이가 h일 때 이진검색트리의 탐색은 O(h)의 시간복잡도를 갖기 때문에 높이가 커지는 경우 실행속도가 점점 늘어나는 것이다.


왼쪽은 바람직한 이진검색트리의 형태. 15개 노드의 높이는 4이므로 최대 4번이면 검색이 가능하다: O(logN)
하지만 오른쪽의 경우 한쪽으로 쏠린 이진 검색 트리의 형태로 15개 노드를 최대 15번 탐색해야 한다: O(N)
위의 오른쪽 그림과 같은 트리가 생기지 않도록, '좌우가 균형잡힌 이진 검색 트리'가 바로 레드 블랙 트리이다. 항상 좌우가 균형잡혀있기 때문에 레드블랙트리의 연산(검색, 전위 순회, 후위 순회, 삽입, 삭제 등)은 최악의 경우에도 O(logN)의 시간 복잡도로 수행할 수 있다.
레드블랙트리의 노드는 일반 이진검색트리의 노드가 가진 key, 부모 노드(p), 왼쪽 자식노드(left), 오른쪽 자식노드(right) 필드 외에 노드의 색깔(color)을 표현하는 한 비트의 추가 기억 공간을 더 가진다. 레드 블랙트리는 루트에서 리프까지의 경로에 나타나는 노드의 색깔을 제한함으로써 경로의 길이들을 비슷하게 맞춰나가고 이로써 트리가 근사적으로 균형을 이룬 트리가 되게 한다.
구체적으로 레드 블랙 트리는 아래 5개 조건을 만족함으로써 근사적으로 좌우가 균형잡힌 이진 검색 트리가 될 수 있다.
🔔 모든 노드는 RED 또는 BLACK
🔔 루트 노드는 BLACK
🔔 모든 리프*(NIL)은 BLACK
🔔 임의의 노드가 RED면 그 노드의 자식은 모두 BLACK (다르게 말하면 RED 노드끼리는 인접 불가)
🔔 임의의 노드로 부터 모든 자손 리프들로 가는 경로들은 모두 같은 수의 BLACK 노드를 포함 (자기 자신은 제외) **
* 세번째 조건의 모든 리프(NIL)를 리프를 자식노드로 갖고있는 노드와 혼동해서는 안 된다! 레드블랙트리에서는 자식이 없는 노드를 NIL이라는 노드를 가진 것으로 표현하기 때문에, 리프 노드는 자식이 없는 노드가 아닌 NIL노드이다. 자세한 내용은 아래의 경계 노드 내용을 참고하면 되고, 우선 여기서 리프는 NIL 노드를 의미한다는 사실을 잘 기억하고 있으면 된다.
** 다섯번째 조건은 아래 blackheight 에서 더 자세히 다루도록 하겠다.
경계노드 T.nil
레드블랙트리 코드에서는 노드가 자식이 없을 때 (노드.left = NIL, 노드.right= NIL 과 같은 노드) 노드의 NIL 자식을 표현하기 위해 경계노드를 이용한다. 아래 그림의 NIL이 쓰인 BLACK 노드들이 바로 레드블랙트리 세번째 조건에서 말하는 리프(NIL)들이다. 이렇게 경계노드를 이용함으로써 노드의 NIL 자식을 정상적인 자식 노드와 동일하게 다룰 수 있게 된다. 경계노드 nil도 다른 노드들과 똑같이 key, 색(color), 부모 노드(p), 왼쪽 자식노드(left), 오른쪽 자식노드(right) 필드를 가지지만 그 값들은 의미가 없다.

하지만 이렇게 수많은 NIL을 각각 표현하는 것은 메모리 낭비이다. 따라서 레드블랙트리 코드에서는 여러 NIL을 한번에 표현하기 위해 하나의 경계노드(sentinal) T.nil을 사용한다. NIL을 자식으로 갖는 모든 노드는 경계노드 T.nil를 가리킨다. (아래 그림 참고)

이해를 돕기 위해 경계노드를 포함하여 레드블랙트리를 그렸지만, 실제로 레드블랙트리에서 경계노드가 가진 필드 값은 중요치 않으므로 트리를 그릴 때 경계노드는 포함하지 않도록 한다.
흑색 높이 (black-height)
흑색 높이는 한 노드 x에서 x의 자손 리프까지의 경로에 있는 모든 흑색 노드(x 자신은 제외, 리프노드는 포함)의 개수를 의미하고 bh(x)로 표시한다. 레드블랙트리의 특징 (다섯 번째 특징) 덕분에 임의의 노드에서 모든 자식 리프까지의 경로에 있는 모든 흑색노드의 수는 동일하기 때문에 bh(x)와 같이 나타낼 수 있다. 참고로 레드블랙트리의 흑색 높이는 루트의 흑색높이로 정의된다.
몇 가지 예시를 들어 흑색 높이를 확인해보자. 아래와 같은 레드블랙트리가 있다.
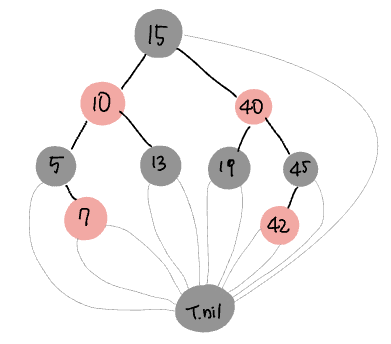
여기서 40이라는 값을 가진 노드를 x라고 할때, bh(x)를 구해보자. 노드 x에서 리프(T.nil) 까지 가는 경로는 5개이다. 아래 그림에서 파란색으로 경로를 표시해두었다. 레드블랙 트리의 다섯번째 특징으로 인해 이 다섯개 경로의 흑색 높이는 2이다. (경로 1,2의 경우 19와 nil 의 두 개, 경로 3,4,5의 경우 45와 nil 의 두 개)

10의 값을 가진 노드를 x라고 해서 bh(x)도 2이다. 5와 nil 또는 13과 nil을 흑색노드로 가지고 있기 때문이다.

레드 블랙 트리의 높이
레드블랙트리의 노드가 n개라면 이 트리의 높이는 최대 2 * log(n+1) 이다. (증명이 궁금하신 분들은 이 곳에서 Proof of bounds 파트를 참고하시길) 따라서 이진 검색트리의 높이가 h 일때 탐색의 시간복잡도는 O(h)이므로, 레드블랙트리 탐색의 시간복잡도는 O(logn)이다.
회전 (rotation)
회전은 레드블랙트리를 만드는 데 아주 중요한 과정이다. 기본적으로 레드블랙트리는 한쪽으로 쏠리지 않은, 균형잡힌 트리이다. 따라서 한쪽으로 트리가 쏠렸을 때 이진검색트리의 특징(왼쪽 자식<=부모<=오른쪽 자식)을 위반하지 않으면서도 트리의 균형을 맞출 수 있는 방법이 바로 회전이다.
간단한 예로, 아래 왼쪽 트리는 이진검색트리이지만 한쪽으로 쏠린, 균형잡히지 않은 이진검색 트리다. 이를 왼쪽으로 회전하면, 오른쪽 트리와 같이 이진검색트리의 특징을 위반하지 않으면서도 트리의 균형을 맞출 수 있게 된다.


트리에 노드를 삽입하거나 삭제하는 연산은 트리를 수정하기 때문에, 삽입과 삭제 이후에는 트리 내 일부 노드들의 색깔과 포인터(다음 노드를 가리키는 변수)를 변경해야 계속해서 레드블랙트리의 특성을 유지할 수 있다. 이때 노드들의 포인터를 변경하기 위해서 '회전'을 사용할 수 있다. 회전에는 좌회전(left-rotate)과 우회전(right-rotate)이 있는데 좌회전을 예를 들어 회전을 이해해보자.

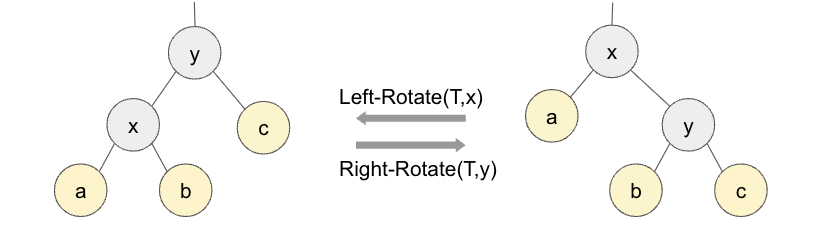
다음과 같이 x,y 노드와 각각의 자식 노드인 a와 b,c 노드가 있는 그래프를 생각해보자.
이 그래프에서 x 노드를 기준으로 좌회전을 해보려고 한다.
** a,b,c는 노드라고 이해해도 되지만, 정확히는 a,b,c노드를 루트로 하는 서브트리라고 이해하는게 더 정확하다.

이 그래프를 진짜 왼쪽으로 90도 돌리면 (!!?) 안되고!!!!!

제대로 좌회전을 하면 이과 같은 그래프 형태가 된다.
형태 자체는 사실 그래프를 왼쪽으로 90도 돌린 위의 그래프와 유사하지만 노드들의 구성이 다르므로 헷갈리지 말도록. 그러면 어떻게 그래프가 바뀌었는지 확인해보자.
y는 x의 오른쪽 자식노드였는데(x<=y), 좌회전 후 x가 y의 왼쪽 자식노드가 되었다. x<=y 에 어긋나지 않는다.
a와 c는 각각 x의 왼쪽 자식노드, y의 오른쪽 자식 노드였는데, 좌회전 후 그대로 유지되고 있다.
b는 x의 오른쪽 자식노드 y의 왼쪽 자식노드였는데(x<=b<=y), 좌회전 후 x의 오른쪽 자식노드가 되엇다. x<=b<=y 에 어긋나지 않는다.
이렇게 회전의 특성은 이진검색트리의 특성 (왼쪽 자식 노드 <부모노드< 오른쪽 자식노드)을 보전한다. 우회전은 좌회전과 대칭으로 움직일 뿐 동일하게 이진검색트리의 특성을 보전한다. 아래의 그림과 같이 x에 대해 좌회전 한 그래프를 y에 대해 우회전하면 원래의 그래프이다.
이제 회전의 대략적인 개념을 이해했으니 좀 더 자세하게 회전이 이루어지는 과정을 살펴보고자 한다.
Left-Rotate(T,x)
Left-Rotate(T,x)는 x에 대해 좌회전을 하겠다는 의미이다. 이때의 x는 오른쪽 자식이 T.nil이 아닌 모든 노드에 해당한다.
좌회전은 x와 x의 오른쪽 자식 y를 연결하는 간선을 중심축으로 하므로 y는 서브 트리의 새로운 루트가, x는 y의 왼쪽 자식이, y의 왼쪽 자식은 x의 오른쪽 자식이 된다. 이때 각 노드의 서브트리까지 함께 이동하게 되는 방식임을 기억하자. 이를 구현하는 의사코드를 살펴보자 (단, 아래 의사코드에서는 x의 오른쪽 자식노드가 NIL이 아니라고 가정)
/* Left-Rotate(T,x) Pseudo Code
각 노드의 p는 노드의 부모 노드를 가리키는 포인터
각 노드의 right은 오른쪽 자식노드를 가리키는 포인터
각 노드의 left는 왼쪽 자식노드를 가리키는 포인터
*/
y= x.right ; // x의 오른쪽 자식노드를 y라는 변수로 설정
x.right = y.left ; // y의 왼쪽 자식노드를 x의 오른쪽 자식 자식노드로 설정
if y.left != T.nil
y.left.p = x ; // 이때 y의 왼쪽 자식노드(b)가 nil이 아니면 y의 왼쪽 노드의 부모노드를 x로 설정
y.p = x.p ; // x의 부모 노드를 y의 부모로 설정
if (x.p == T.nil)
T.root = y ; // x의 부모노드가 nil이라면(x가 루트노드라면) 트리의 root를 y로 설정
else if (x == x.p.left)
x.p.left = y ; // x가 부모노드의 '왼쪽'노드라면, x의 부모노드의 왼쪽 노드를 y로 설정
else
x.p.right = y // x가 부모노드의 '오른쪽'노드라면, x의 부모노드의 오른쪽 노드를 y로 설정
y.left = x // y의 왼쪽노드를 x로 설정
x.p = y // x의 부모노드를 y로 설정
각 코드를 실행할때마다 트리와 노드가 어떻게 변해가는지 line by line으로 정확히 짚어보도록 하자.
T는 아래와 같은 그래프와 같다고 하자. x의 오른쪽 자식노드 포인터 값이 가리키는 노드를 y라고 한다.
y= x.right ;
x의 오른쪽 자식노드 값에 y의 왼쪽 자식노드 값을 대입한다.
x.right = y.left ;

이때 y의 왼쪽 자식노드가 nil이 아니면 y의 왼쪽 노드의 부모노드 값을 x로 설정
if y.left != T.nil
y.left.p = x ;
y의 부모노드 값에 x의 부모노드값을 대입한다.
y.p = x.p ;
x가 루트노드인지, 왼쪽 자식인지, 오른쪽 자식인지에 따라 트리의 root값을 수정하거나, x의 부모노드 값을 수정한다. 우리가 예시로 들고 있는 트리 T에서 x는 루트 노드이므로 트리의 root를 y로 수정한다.
if (x.p == T.nil)
T.root = y ; // x의 부모노드가 nil이라면(x가 루트노드라면) 트리의 root를 y로 설정
else if (x == x.p.left)
x.p.left = y ; // x가 부모노드의 '왼쪽'노드라면, x의 부모노드의 왼쪽 노드를 y로 설정
else
x.p.right = y // x가 부모노드의 '오른쪽'노드라면, x의 부모노드의 오른쪽 노드를 y로 설정
이제 y의 왼쪽 노드 값을 x로, x의 부모노드 값을 y로 설정하면 좌회전이 모두 완료된다.
y.left = x // y의 왼쪽노드를 x로 설정
x.p = y // x의 부모노드를 y로 설정
이렇게 트리를 회전해도 이진검색트리의 특성은 그대로 유지되고, 회전하기 전과 회전한 후의 이진검색트리 중위 순회의 결과는 같다. 아래의 그림은 11의 값을 가진 노드를 대상(x)으로해서 Left-Rotate(T,x)를 시행하기 전, 후의 그래프를 보여준다. 위의 그래프를 중위 순회한 결과와 아래의 그래프를 중위순회한 결과는 모두 2-3-4-6-7-9-11-12-14-17-18-19-20-22 로 동일하다.

C언어로 구현하기
좌회전 수행 코드
void left_rotate(rbtree *t, node_t *x) {
node_t *y = x->right;
x->right = y->left;
if (y->left != t->nil)
y->left->parent = x;
y->parent = x->parent ;
if (x->parent == t->nil)
t->root = y ;
else if (x == x->parent->left)
x->parent->left = y;
else
x->parent->right = y;
x->parent = y ;
y->left = x ;
}우회전 수행코드
void right_rotate(rbtree *t, node_t *x) {
node_t *y = x->left;
x->left = y->right;
if (y->right != t->nil)
y->right->parent = x;
y->parent = x->parent ;
if (x->parent == t->nil)
t->root = y ;
else if (x == x->parent->left)
x->parent->left = y;
else
x->parent->right = y;
x->parent = y ;
y->right = x ;
}
레드블랙트리의 개념과 용어를 살펴보았고, 이를 바탕으로 연산을 수행하기 위해 필요한 회전 방법에 대해 알아보았다. 다음 포스팅에서는 레드블랙트리의 삽입/삭제 를 다루어보겠다.
Reference
1. Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein, 『Introduction to Algorithms, 3rd Edition (The MIT Press)』, 문병로, 심규석, 이충세 , 한빛 아카데미, 2014
'TIL' 카테고리의 다른 글
| [OS] pintos의 interrupt frame 이란 + do_iret 함수가 하는 일 (0) | 2022.11.29 |
|---|---|
| [OS] Pintos - system call 호출 및 흐름 (0) | 2022.11.25 |
| 백준 11049. (PyPy3 1등 먹은 풀이!) 행렬체인곱셈 | Python 다이나믹 프로그래밍 (0) | 2022.10.19 |
| 백준 11047. 동전 0 | Python | 그리디 (0) | 2022.10.15 |
| 백준 1904. 01타일 | Python | 메모이제이션 & 바텀엄(상향식) 접근 방식 풀이 (0) | 2022.10.15 |




댓글