🔔 문제 설명은 백준 문제 링크로 대신합니다
11049번: 행렬 곱셈 순서
첫째 줄에 입력으로 주어진 행렬을 곱하는데 필요한 곱셈 연산의 최솟값을 출력한다. 정답은 231-1 보다 작거나 같은 자연수이다. 또한, 최악의 순서로 연산해도 연산 횟수가 231-1보다 작거나 같
www.acmicpc.net
수많은 시도 끝에 성공한 행렬체인곱셈 문제.. CLRS 책을 한참 읽고서야 이해했고, 문제를 푸는 데도 한참이 걸렸던 문제다. 이 문제는 제대로 상세히 기록을 해 둬야 할 것 같다!!
처음에는 하향식 + 메모이제이션으로 풀었는데 계속해서 시간초과가 났다. 이 문제를 먼저 맞춘 팀원들은 다 상향식으로 풀었다고 해서 상향식으로 다시 풀었다. 사실 CLRS에서 상향식으로 푸는 부분은 도저히가 이해가 안가서 하향식으로 풀었던 건데 ㅠㅠ 다행히 JH가 상향식으로 푸는 방법에 대해서 간단히 설명을 해줘서 그 설명을 듣고나서 상향식으로 접근해볼 수 있었다.
오랜 시간을 걸려 상향식으로 문제를 풀어냈는데 또 시간초과가 났다. 머리에서 김이 모락모락 나고있는데 JH가 pypy로 돌려보라고 했다. pypy로 제출했더니 ‘채점중’ 에서 변하지 않는다. 망했네하던 순간 갑자기 1% 오름 ㅎㅎ 어!? 하는데 또 1%로 오름.. 그렇게 한 5분 정도 채점하더니 4836ms이라는 무시무시한 결과가 나왔다
원래 이 정도 시간이 나오는 게 맞는건가해서 JW에게 물어보니 680ms 정도가 나왔다고 한다. 그러면 내 코드는 8배가 느린 건데 … 🥲 우리반 시간복잡도 다이어트 장인들의 몇 가지 조언을 따라 코드를 수정하고 돌려보니 갑자기 시간이 11배는 줄어들어서 392ms가 나왔다. 애들이 랭킹을 보라고 했더니 2위!!!!!!!!!!!! 백준은 돌릴때마다 시간이 조금씩 다르기 때문에 그냥 한번 더 돌려봤더니 이번에는 384ms가 나와서 1위가 됐다 ㅋㅋㅋㅋ

그렇다면 이제 부터 스압 주의. 행렬체인 곱셈을 어떻게 풀어냈는지, 중간에 코드를 어떻게 수정했길래 갑자기 11배가 줄어들 수 있었던건지에 대해 각 과정을 상세히 기록해보겠다!!!
행렬 체인 곱셈이란?
행렬의 곱셈에는 결합 법칙이 성립한다. 행렬 A, B, C를 곱할 때 (A*B)*C 순서대로 곱하나, A*(B*C) 순서대로 곱하나 결과는 동일하다. 하지만 (A*B)*C 순서대로 곱할 때와, A*(B*C) 순서대로 곱할 때의 계산의 수는 다르다.
백준 문제의 예시를 그대로 가져와보자면, A의 크기가 5×3이고, B의 크기가 3×2, C의 크기가 2×6인 경우 :
✏️ (AB)C 에 필요한 곱셈 연산의 수는 5×3×2 + 5×2×6 = 30 + 60 = 90번
✏️ A(BC) 에 필요한 곱셈 연산의 수는 3×2×6 + 5×3×6 = 36 + 90 = 126번
그렇다면 $A_1*A_2*A_3... A_{n-1}* A_n$ 과 같이 n개의 행렬을 곱할 때, 어떻게 괄호를 묶어야 곱셈연산을 최소로 할 수 있을지를 구하는 문제가 행렬 체인 곱셈 문제이다. 백준 11049번 문제는 이때의 최소곱셈 연산 수를 출력해야 한다.
괄호 묶는 방법의 수
우선 $A_1*A_2*A_3... * A_n$ 의 행렬의 곱셈에서 괄호를 묶는 방법은 몇 가지가 있는지를 생각해보자.
우선 P(n)을 n개의 행렬의 곱셈에서 괄호를 묶는 방법의 수 라고 정의하겠다.
P(1)의 경우 행렬이 1개일 때 괄호를 묶는 방법의 수이다. A 라는 행렬 하나가 있을 때 괄호는 (A) 로 밖에 묶이지 않는다. 즉 P(1)= 1 이다.
P(n)에서 n이 2 이상인 경우 P(n)은 두 개의 완전하게 괄호로 묶인 두 부분들의 괄호를 묶는 방법의 수의 곱이라고 생각할 수 있다.
예를 들면, P(2)의 경우 행렬이 2개일 때 괄호를 묶는 방법의 수이다. 행렬의 곱 AB는 (A)(B)로만 둘로 나누어질 수 있는데, AB를 괄호로 묶는 방법의 수는 A를 괄호로 묶는 방법의 수 * B를 괄호로 묶는 방법의 수일 것이다. 우리는 P(1) = 1 라는 것을 이미 알고 있기 때문에 A를 괄호로 묶는 방법의 수 = 1, B를 괄호로 묶는 방법의 수 = 1 라는 것을 알 수 있다. 따라서 P(2) = 1*1 = 1이다.
P(3)의 경우 조금 더 생각해야 한다. 행렬이 3개인 경우는 두개의 괄호로 묶는 경우가 2 가지이다. 괄호로 묶인 두 부분을 (A)(BC) 이렇게 만들 수도 있고, (AB)(C) 이렇게 두 부분으로 만들 수도 있다. 이 두 가지의 경우를 모두 더해야 한다. 다행히 우리는 P(1)도 알고 P(2)도 알기 때문에 (A)(BC)는 P(1)*P(2)= 1 라는 것을 금방 계산할 수 있고, (AB)(C)는 P(2)*P(1) = 1 이라는 것도 금방 계산할 수 있다. 따라서 P(3)= P(1)*P(2)+ P(2)*P(1) = 2 이다.
P(3)을 보면서 한 가지 패턴을 더 알아낼 수 있다. P(3)에서 두 개의 완전하게 묶인 괄호 사이의 경계선은 첫번째 행렬 뒤에서 한 번, 두번째 행렬 뒤에서 한 번 있었다. 행렬의 수가 n개라면, 이 경계선은 1번 행렬 뒤에서 한 번, 2번행렬 뒤에서 한 번, … , n-1 번 행렬 뒤에서 한 번. 총 n-1 개가 있을 것이다. 우리는 이 각각의 경계선을 기준으로 앞뒤를 괄호로 묶어 완전한 두 개의 행렬로 만들고, 각각의 경우를 계산하여 합치면 된다.
그래서 아래와 같은 패턴을 발견할 수 있다.
P(1)= 1
P(2) = P(1)*P(1)
P(3) = P(1)*P(2) + P(2)*P(1)
P(4) = P(1)*P(3) + P(2)*P(2) + P(3)*P(1)
…
P(n) = P(1)*P(n-1) + P(2)*P(n-2) + … + P(n-1)*P(1)
즉, P(n)은 $\Sigma^{n-1}_{k=1} P(k)P(n-k)$ 이다. (그냥 한 번에 표시하려니까 이런 공식인 거지 P(n)이 어떻게 계산되는 건지에 대한 과정만 이해했다면 된다고 생각한다.)
행렬의 곱
고등학교 수학에서 다뤘던 행렬의 곱을 잠시만 떠올려보자. 여담이지만 정글에서 24,25 살 동생들에 따르면 이제 고등학교 교육과정에는 행렬을 안배운다고 하던데 ..!? 세상에!
A행렬이 P행 Q열, B 행렬이 Q행 R열이라고 하면, B*A 방식으로는 계산할 수 없다. 앞 행렬의 열 갯수와 뒤 행렬의 행 갯수가 같을 때만 행렬을 곱할 수 있기 때문이다. 즉 A*B는 계산이 가능하고 이때 계산의 결과로 나온 행렬을 C 행렬이라고 하면, C행렬은 P행 R열을 갖고 있다. 그리고 이때 곱셈 연산의 수는 P*Q*R 개이다.
간단하게 예시를 보자.

앞 행렬은 1X3 행렬, 뒤 행렬은 3X2 행렬이고, 앞 행렬의 열 = 뒤 행렬의 행 이므로 곱셈 연산이 가능하다. 계산 결과로 나온 행렬은 1X2 행렬이다. 곱셈 연산의 수는 1*3*2인 6이다.
이를 토대로 한 가지만 더 생각해보자.
$A_1*A_2*A_3... * A_n$ 의 n개의 행렬을 순서대로 곱할 수 있다고 할 때, 두번째 행렬부터 맨 뒤까지의 모든 행렬은 항상 자신의 앞 행렬의 열 수를 행 수로 갖고 있을 것이다. 따라서 $A_1*A_2*A_3... * A_n$ 에서 각각의 행렬의 행, 렬 정보를 수열 p로 표현할 수 있고, p = {$A_1$ 행 수, $A_1$ 열 수(=$A_2$ 행 수), $A_2$ 열 수(= $A_3$ 행 수) , … , $A_{n-1}$ 열 수(= $A_n$ 행 수), $A_n$ 열 수} 이 수열을 통해 행렬의 정보를 아래와 같이 나타낼 수 있다.
$A_1*A_2*A_3... * A_n$ 에 대해 $A_i$ 는 $p_{i-1}*p_{i}$ 차원의 행렬이다. (i)
행렬체인 곱셈
이제 행렬 체인 곱셈을 해결하기 위한 모든 준비가 마쳐졌다 ! 행렬체인 곱셈 문제는 대표적인 DP 문제이다. 즉, 부분 문제에 대한 최적 해를, 큰 문제에 대한 최적 해를 구하는데 사용한다.
우리가 구해야 하는 값은 $A_1*A_2*A_3... * A_n$ 에서 최소의 곱셈 연산 수이다. 이 행렬 곱셈 문제를 어떻게 ‘부분 문제’로 나눌 수 있을까? (힌트는 위에서 다룬 ‘괄호 묶는 방법’이다.)
$A_i*A_{i+1}*A_{i+2}... A_{j-1}*A_{j}$의 행렬의 곱셈을 두 개의 괄호로 완전히(=괄호 밖에 있는 행렬이 없도록) 묶어서 두 행렬의 곱으로 만들어보자. i와 j사이의 어떤 k값을 기준으로 행렬을 구분한다면 $A_i*A_{i+1}*A_{i+2}... A_{j-1}*A_{j}$는 아래와 같은 두개의 행렬의 곱으로 표현할 수 있을 것이다.
$A_i*A_{i+1}*A_{i+2}... A_{j-1}*A_{j}$ = ($A_i*A_{i+1}*A_{i+2}... A_{k-1}*A_{k}$)*($A_{k+1}*A_{k+2}... A_{j-1}*A_{j}$)
$A_i*A_{i+1}*A_{i+2}... A_{j-1}*A_{j}$의 곱셈 연산 수 를 라고 해보자. 그렇다면 이 정의에 따라서 는 k를 기준으로 구분한 두 행렬 각각의 곱셈 연산 수 + 이 두 행렬을 곱하는 곱셈 연산 수일 것이다.
즉
m[i,k] (i번 행렬 ~ k번 행렬까지의 곱셈 연산 수)
+ m[k+1, j] (k+1번 행렬 ~ j번 행렬까지의 곱셈 연산 수)
+ (i번 행렬 ~ k번 행렬을 곱한 결과 행렬) * (k+1번 행렬 ~ j번 행렬을 곱한 결과 행렬)의 곱셈 연산 수
이다.
이제 거의 다 왔다. 저 마지막에 더하는 곱셈 연산수만 구하면 된다. 이 곱셈 연산의 수는 어떻게 구할까 ?
우선 행렬의 특성을 다시 한 번 떠올려보자. 아무리 많은 행렬을 곱해도 최종 결과가 되는 행렬은 곱셈의 첫 행렬의 행, 마지막 행렬의 열의 차원을 가진다. 즉 ($A_i*A_{i+1}*A_{i+2}... A_{k-1}*A_{k}$)의 결과가 되는 행렬은 $A_i$ 행렬의 행 X $A_k$ 행렬의 열 을 가진다. 마찬가지로 ($A_{k+1}*A_{k+2}... A_{j-1}*A_{j}$)의 결과가 되는 행렬은 $A_{k+1}$ 행렬의 행 X $A_j$ 행렬의 열 을 가진다.
이에 따라 곱셈연산의 수는 $A_i$행렬의 행 * $A_k$ 행렬의 열 * $A_j$ 행렬의 열이다.
위에서 다룬 수열 p (행렬의 곱에서 각 행렬의 행,렬 정보를 담은 수열) 을 기억해보자. $A_1*A_2*A_3... * A_n$ 에 대해 $A_i$ 는 $p_{i-1}*p_{i}$ 차원의 행렬이므로, 이를 활용해서 최종적으로 식을 완성해보면 아래와 같다.
$$ m[i,j] = m[i,k] + m[k+1, j] + p_{i-1}*p_i $$
최소의 곱셈 연산
우리가 위에서 정의한 는 $A_i*A_{i+1}*A_{i+2}... A_{j-1}*A_{j}$의 곱셈 연산 수 인데, 사실 우리가 진짜 알고싶은 정보는 $A_i*A_{i+1}*A_{i+2}... A_{j-1}*A_{j}$의 최소 곱셈 연산 수이다. 이 ‘최소’를 구하는 방법만 추가하게 된다면 우리는 이 문제를 진짜 해결할 수 있다! (거의 다 왔어요 포기하지 마세요!!! 진짜 몇 줄 안 남음!)
사실 ‘최소’ 곱셈 연산 수를 구하는 과정은 생각보다 어렵지 않다. 행렬의 곱을 두 그룹으로 묶어주는 기준이 되는 k값은 범위를 가지기 때문에 모든 k값에 대해서 m[i,j]를 계산한 후 이 중 최솟값을 골라주면 그게 바로 최소의 가 된다.
이제 점화식을 정리해보자. 이제 m[i,j]의 정의를 $A_i*A_{i+1}*A_{i+2}... A_{j-1}*A_{j}$의 최소 곱셈 연산 수라고 수정하겠다.
에서 i 라면, 행렬이 하나만 있는 경우로, 곱셈 자체가 이루어 지지않으므로 이다.
i≠j 라면, 는 모든 k에 대해 계산할 수 있는 $ m[i,j]= m[i,k] + m[k+1,j] + p_{i-1}*p_k*p_j $중 최솟값이다.
이를 점화식으로 나타내자면 !
$$ m[i,j] = min (m[i,k] + m[k+1, j] + p_{i-1}*p_i) (i<=k<j)$$
이다.
이제 점화식을 모두 구해냈다! 코드로 만들어내보자.
코드 구현 (python)
dp 테이블
우선 m[i,j] 값을 저장할 수 있어야 한다. 나는 처음에 배열이 아닌 키를 (i,j)튜플로 가지는 dictionary 자료형을 만들었는데, 이게 원흉이었다. 자료형을 dict에서 2차원 배열로 바꾸자마자 속도가 11배가 빨라졌다..
m = [[0]*(N+1) for _ in range(N+1)]m[i,j] 를 저장할 수 있는 2차원 배열을 만들었다. 행렬은 1번째 부터 셀 거라서 m도 편의상 m의 0행 0열을 버리려고 N+1행, N+1열로 만들었다.
for i in range(1,N+1):
m[i][i] = 0 # 초깃값 셋팅 (i=j인 경우들)i와 j가 같은 경우 (행렬이 하나만 있는 경우) m[i][j]는 0 이므로 초깃값으로 0을 먼저 넣어준다.
행렬의 행/렬 정보를 담은 리스트
우리가 만든 점화식은 행렬의 정보를 담은 수열을 바탕으로 한다. 문제에서는 한 줄에 한 행렬의 행 렬 정보가 주어지므로 행렬 정보를 받아서 p 라는 리스트의 원소로 넣어준다. ( p = [ $A_1$ 행, $A_1$열, $A_2$열, … $A_n$열 ] )
p = []
a,b = map(int,input().split())
p.append(a)
p.append(b)
for i in range(1, N):
a,b = map(int,input().split())
p.append(b)
반복문 실행 (상향식 접근 ; bottom up approach)
현재 상황을 생각해보자. 우리는 2차원 배열인 m을 가지고 있고, i=j 인 칸(m[i][j]) 들은 0이라는 값을 가진다. m[i,j]의 정의에 따라 항상 i≤j이므로 i>j인 칸들은 사용되지 않으므로 x표시를 해두었다.
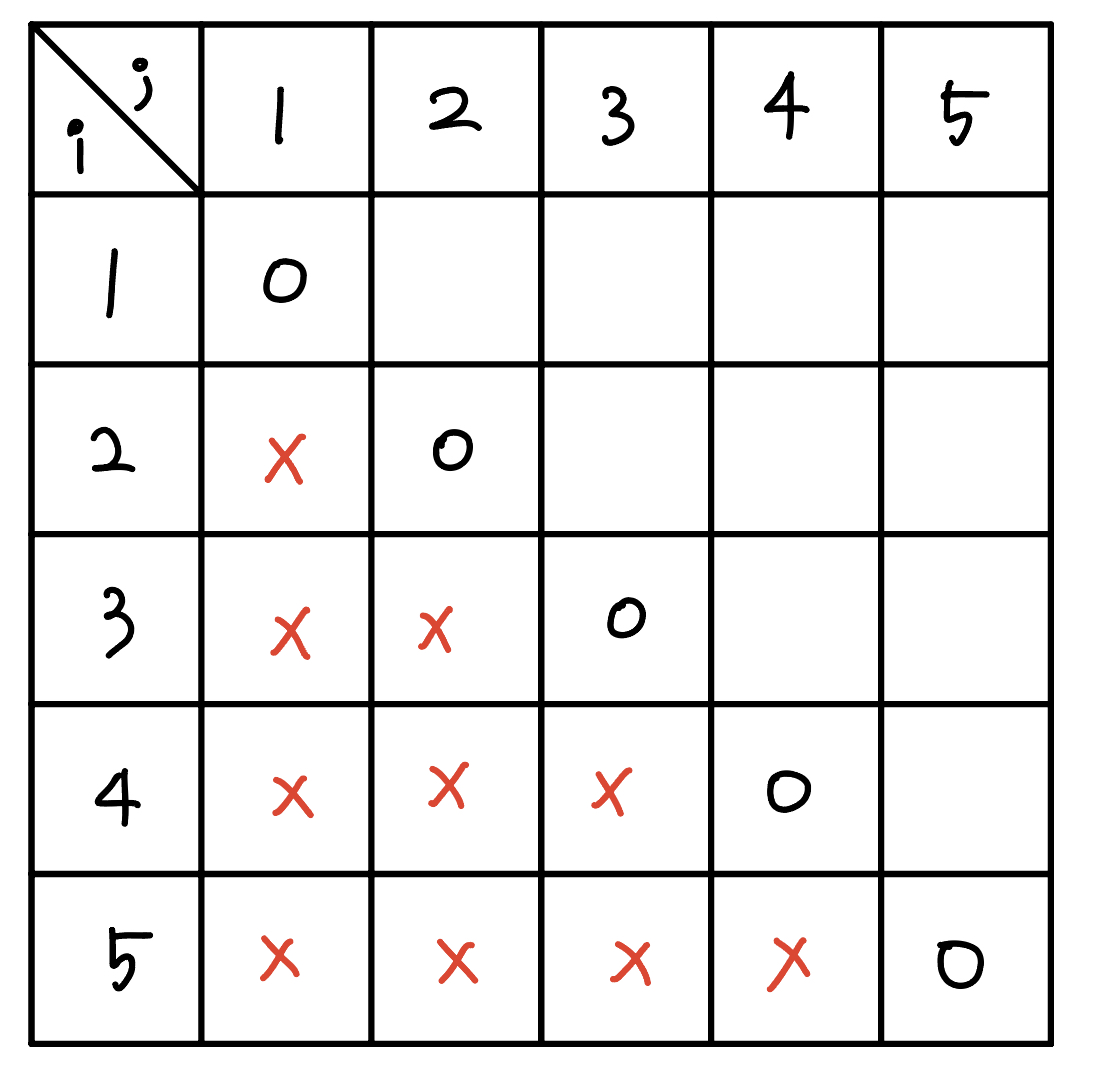
상향식 계산을 어디서부터 해야할 지 알기 위해 먼저 m[1,2]에 해당하는 칸 인 m[1][2]를 계산해보자.
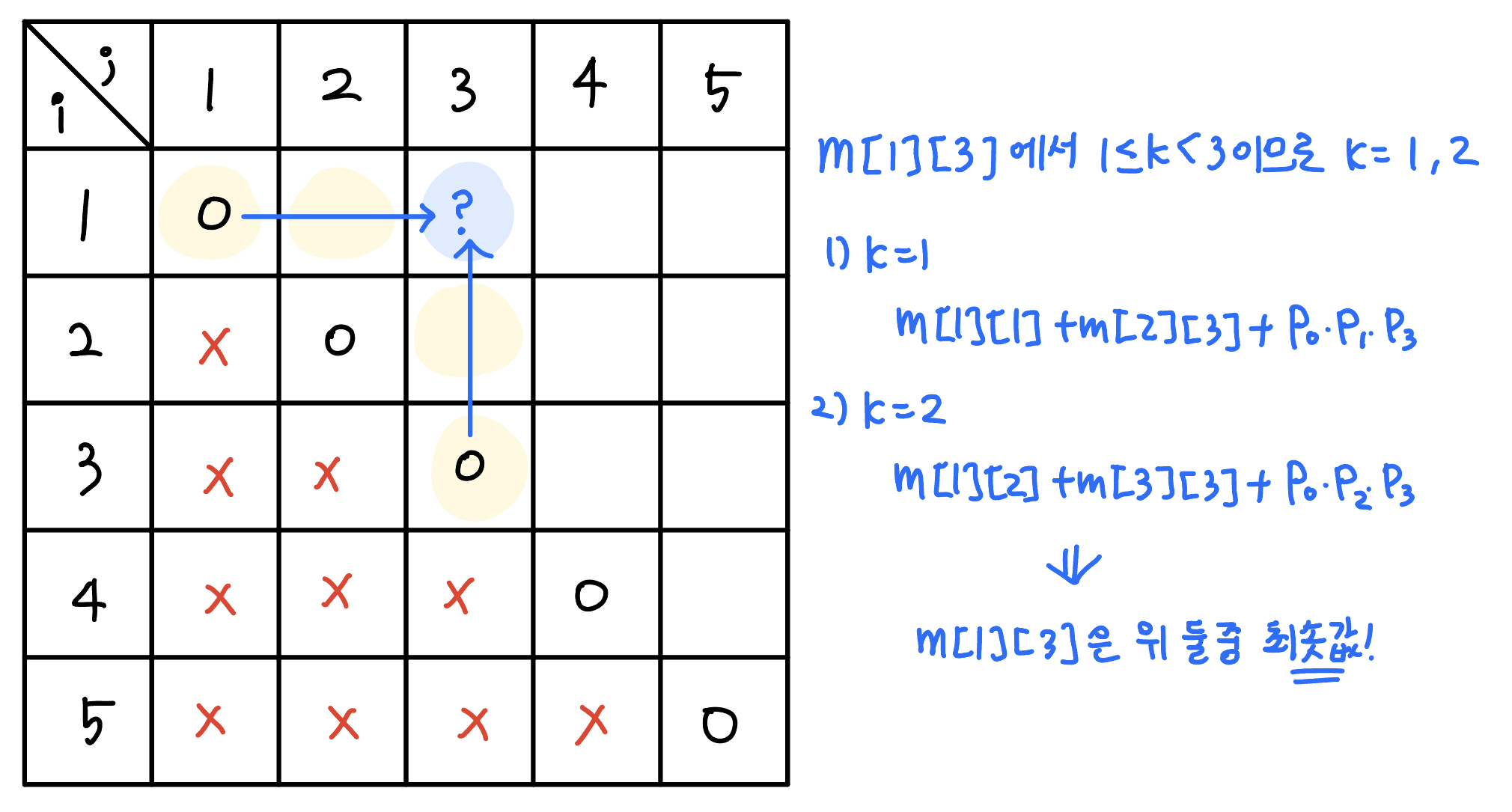
m[1][2]를 계산하기 위해서는 m[1][1]의 값과 m[2][2]의 값이 사용됨을 알 수 있다. m[1][3]도 확인해보자.
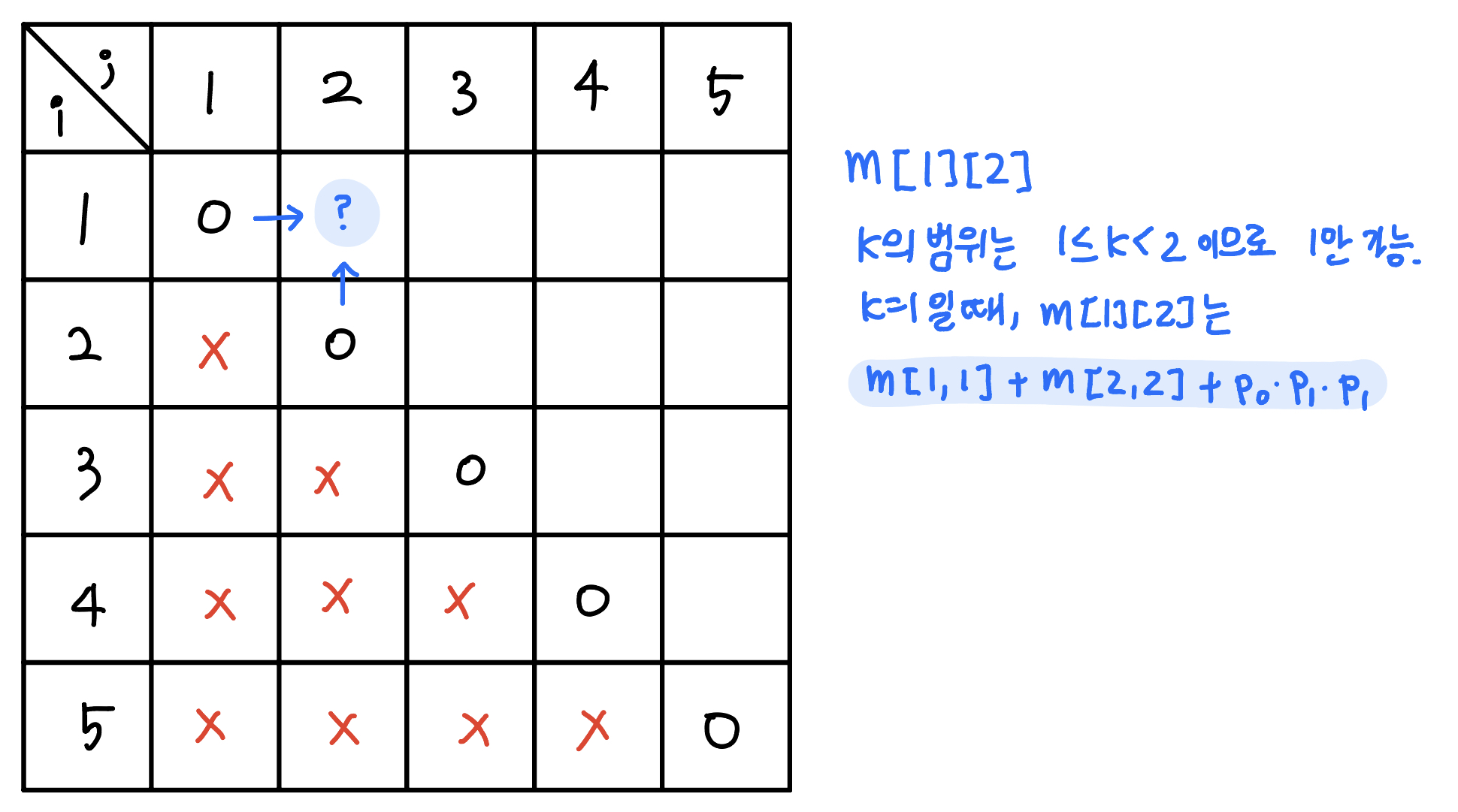
즉, 어떤 값을 계산하려면 그 왼쪽의 값들과 그 아랫쪽의 값들이 먼저 있어야 해당 값들을 이용해서 값을 계산할 수 있다. 위 그림의 예시에서는 1,1 → 2,2 → 1,2 → 3,3 → 2,3 → 1,3 → … → 2,5 → 1,5 순으로 계산해야 한다.
이 순서를 만족하기 위해 j부터 반복문을 돌리고 그 다음 i 반복문을 썼다 (이 range를 가능하게 하느라 머리 빠개지는 줄 알았다 🤯 !!! ) 그때 그때 최솟값을 찾기 위해서 계산 값을 temp에 담아 놓은 후 현재의 최솟값과 비교하여 더 작으면 갱신하고, 계산을 마치면 m 테이블을 업데이트 하도록 했다.
INF = sys.maxsize
for j in range(1, N+1) :
for i in range(j-1, 0,-1) :
min_value = INF
for k in range(i,j) :
temp_value = m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j]
if min_value > temp_value :
min_value = temp_value
m[i][j]= min_value
그렇게 해서 완성된 최종 코드이다.
import sys
input = sys.stdin.readline
INF = sys.maxsize
N = int(input())
m = [[0]*(N+1) for _ in range(N+1)]
p = []
a,b = map(int,input().split())
p.append(a)
p.append(b)
for i in range(1, N):
a,b = map(int,input().split())
p.append(b)
for i in range(1,N+1):
m[i][i] = 0 # 초깃값 셋팅 (i=j인 경우들)
for j in range(1, N+1) :
for i in range(j-1, 0,-1) :
min_value = INF
for k in range(i,j) :
temp_value = m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j]
if min_value > temp_value :
min_value = temp_value
m[i][j]= min_value
print(m[1][N])
계속해서 시간초과를 받는 하향식 코드도 함께 첨부한다. 시간을 줄일 방법이 보이시는 분들은 댓글로 좀.. 알려주세요..
import sys
from collections import defaultdict
sys.stdin = open("input.txt")
input = sys.stdin.readline
memo = defaultdict(int)
N = int(input())
p = []
a,b = map(int,input().split())
p.append(a)
p.append(b)
for i in range(1, N):
a,b = map(int,input().split())
p.append(b)
print(p)
def min_multiply(i,j) :
if i ==j :
memo[(i,j)] = 0
else:
if not memo[(i,j)] : # memo에 키가 없으면 0이니까 not으로 부정연산
min_k = sys.maxsize
for k in range(i,j):
if not memo[(i,k)] :
memo[(i,k)] = min_multiply(i, k)
if not memo[(k+1,j)]:
memo[(k+1,j)]= min_multiply(k+1, j)
temp_k = memo[(i,k)]+memo[(k+1,j)]+p[i-1]*p[k]*p[j]
if min_k > temp_k :
min_k = temp_k
memo[(i,j)] = min_k
return memo[(i,j)]
print(min_multiply(1, N))
한줄 총평: 쉽지 않은, 아니 대빵 어려운 문제였다. CLRS를 보면서 공부해서 그런지 깊이는 있었지만 너무나 어려웠다 ^^: 아직도 dp로 problem을 subproblem으로 쪼개는 부분이 눈에 잘 들어오지 않지만 이 문제를 통해 dp사고력이 +1 되었기를 바라본다!!!
끝.
Reference
Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein, 『Introduction to Algorithms, 3rd Edition (The MIT Press) 3rd Edition』, 문병로, 심규석, 이충세 , 한빛 아카데미, 2014
'TIL' 카테고리의 다른 글
| [OS] Pintos - system call 호출 및 흐름 (0) | 2022.11.25 |
|---|---|
| [자료구조] Red Black Tree (레드 블랙 트리) | 레드 블랙 트리란, 경계 노드, black-height(흑색높이), Left-Rotate(좌회전), Right-Rotate(우회전), C언어 구현 (2) | 2022.10.24 |
| 백준 11047. 동전 0 | Python | 그리디 (0) | 2022.10.15 |
| 백준 1904. 01타일 | Python | 메모이제이션 & 바텀엄(상향식) 접근 방식 풀이 (0) | 2022.10.15 |
| 백준 2748. 피보나치 수 2 | Python | 메모이제이션 & 바텀엄(상향식) 접근 방식 풀이 (0) | 2022.10.14 |




댓글