🔔 정글 교육과정에 따라 malloc 패키지를 사용하지 않고 직접 동적 메모리 할당기를 구현하는 과정에서
공부한 동적 메모리 할당기 이론 및 코드들을 정리하는 포스팅입니다.
" CS:APP (북미판, 글로벌에디션, 한국어 모두 참고) 9.9 장을 공부하며 작성한 글이기 때문에 정보를 드리기 위함보다는
공부한 내용을 정리하기 위한 포스팅이기 때문에 독자들이 읽기에 가독성이 떨어질 수 있음을 미리 알려드립니다 🔔
🚨 1워드가 몇 바이트 인지는 CPU에 따라 다르기 때문에 CS:APP 9장 및 본 포스팅에서는 1워드를 4바이트라고 가정합니다 🚨
C 프로그래머들은 프로그램을 실행하는 중에(runtime) 추가적인 가상 메모리가 필요할 때 동적 메모리 할당기(dynamic memory allocator)를 사용하는 것이 저언어(e.g. mmap, munmap 함수) 를 사용하는 것보다 간편하다고 생각했다.
동적메모리 할당기는 프로세스의 가상메모리의 heap 영역을 관리하는데, heap 영역은 uninitialized data 영역이 끝난 바로 다음부터 시작하고, 주소가 올라가는 방향으로 커진다. 즉 주소값이 커짐으로서 크기가 커지는 것이다. 아래 그림은 리눅스 프로세스의 가상메모리 구조인데, Uninitialized data 바로 다음 (바로 위) Run-time heap이 위치하고 있는 것을 알 수 있다. 또한 그림에서 알 수 있듯이 각각의 프로세스에 대해서 커널은 변수 brk를 사용해서 heap의 가장 위를 가리키도록 한다. (*커널은 SW과 HW를 이어주는 역할)

할당기는 heap을 다양한 사이즈의 블록들의 모음으로 관리한다. 각각의 블록은 가상 메모리에서 연속적으로 이어지는 메모리들의 덩어리 라고 생각할 수 있고, 이 각각의 블록은 할당(allocated)상태이거나 가용(free) 상태이다.
allocated block, 즉 할당된 블록이란 사용처가 정해진 메모리 블록이다. 응용프로그램이 사용하기 위해서 명시적으로 찜해놓은 블록이다.
free block, 즉 가용 블록이란 이 역시 말그대로 가용 (= 사용 가능한) 메모리 블록이다. 즉 아직 어떤 값이 할당되지 않은 상태이기 때문에 할당될 수 있는 상태의 블록이다.
할당된 블록이 해제(free)되면 가용 블록이 되고, 가용 블록이 할당(allocate) 되면 할당된 블록이 된다. 방금 할당된 블록이 해제되면 가용 블록이 된다고 했는데 해제에는 두 가지 방법이 있고, 할당기는 이 해제 방법에 따라 명시적 할당기와 묵시적 할당기로 구분된다.
명시적 할당기는 명시적으로 블록을 할당하고, 명시적으로 블록을 해제 한다. 동적메모리 할당에 사용되는 C언어의 malloc패키지가 명시적 할당기에 해당한다. (malloc으로 할당 & free로 해제) 반면, 묵시적 할당기는 명시적으로 블록을 할당하고, 별도로 블록을 해제하지는 않는다. 대신에 할당기는 사용되지 않는 할당된 블록을 자동으로 탐지해서 해제를 해준다. Java 등의 가비지콜렉터(garbage collector)가 묵시적 할당기에 해당한다.
C 표준라이브러리는 명시적 할당기인 malloc 패키지를 제공한다. malloc 패키지의 malloc 함수를 호출하면 heap의 블록을 할당할 수 있고, free 함수를 사용하면 할당된 블록을 해제할 수 있다. (malloc 함수는 [말록] 이라고 읽는다. 그런데 calloc은 [씨얼록] 이라고 읽는다.. 신기..)
malloc, calloc, realloc
#include <stdlib.h>
void *malloc(size_t size);malloc 함수는 위와 같이 사용한다. 함수 앞에 void * 를 통해 예측할 수 있듯이 malloc 함수는 heap의 블록을 할당한 후, 할당된 블록을 가리키는(블록의 가장 첫 바이트를 가리키는) 포인터를 반환한다. 만약 메모리 부족 등으로 할당에 실패할 경우에는 NULL을 반환한다. malloc 함수는 반환하는 메모리를 초기화하지는 않으며, 메모리 할당과 함께 메모리를 초기화 하고 싶은 경우 malloc 함수와 비슷한 calloc 함수를 사용하면 된다. 또한 이미 할당된 메모리의 크기를 변경하고 싶은 경우 realloc 함수를 사용하면 된다.
동적메모리 할당기가 메모리를 할당하는 과정
malloc 함수는 인자로 할당할 바이트 크기(size)를 받는다. 하지만 1바이트 할당 요청을 받는다고 1바이트를 할당하고, 2바이트 할당을 요청 받는다고 2바이트를 할당하는 식으로 메모리를 할당하는 것이 아닌, 메모리 정렬에 따라 메모리를 할당한다. (메모리 정렬에 대해서는 직접 정리하기 보다는 잘 설명해둔 블로그 링크를 추가하고 넘어가려고 한다. 나중에 따로 포스팅 할 수 있을 때가 오겠지..) 본 포스팅에서는 double-word 정렬을 기준을 가정하였다.
메모리 얼라인먼트(Memory Alignment)
메모리 얼라인먼트는 레퍼런스마다 데이터 구조 얼라인먼트(Data Structure Alignment), 데이터 얼라인먼트(Data Alignment) 등으로 불리기도 하며, 위키피디아에서는 다음과 같이 개요가 작성되어 있습니
minusi.tistory.com
결국 malloc은 인자로 받은 size를 가지고, 메모리 정렬에 어긋나지 않는 최소의 바이트의 메모리를 할당한 후 이를 가리키는(=할당한 블록의 첫 바이트 주소를 가리키는) 포인터를 할당한다. malloc이 반환하는 포인터는 32비트에서는 8의 배수, 64비트에서는 16의 배수이다.
malloc 함수와 같은 동적메모리할당기는 mmap함수와 munmap 함수를 사용하여 heap 메모리를 명시적으로 할당할 수도 있고, sbrk 함수를 사용할 수 도 있다. 위에서 커널의 변수 brk 는 힙의 맨 위를 가리키는 포인터라고 했는데, sbrk 함수는 이 brk포인터의 값에 incr 값을 더함으로서 heap 영역의 크기를 늘리거나 줄인다.
#include <unistd.h>
void *sbrk(intptr_t incr);sbrk 함수는 성공적으로 heap의 사이즈를 늘린 경우 기존 brk 값(아래 그림의 oldbrk)을 리턴하고, 수행에 실패한 경우 -1 을 리턴한다.

free
malloc, calloc, realloc 등으로 할당된 메모리를 해제할 때는 free 함수를 호출한다.
#include <stdlib.h>
void free(void *ptr);free 함수는 해제할 블록의 첫 바이트를 가리키는 포인터 ( = malloc, calloc, realloc에서 리턴받은 포인터 값) 를 인자로 받는다. 다른 곳을 가리키는 포인터를 받으면 아무것도 하지 않는다. free 함수는 성공해도, 실패해도 아무런 값도 리턴해주지 않기 때문에 알 수 없는 런타임 에러들을 만들어내므로 주의해야 한다.
malloc과 free 함수로 블록을 할당하고 해제하는 과정
아래 그림을 통해 블록이 할당되고 해제되는 과정을 더 잘 이해할 수 있다. 아래 그림에서 각각의 정사각형은 1워드 (=4바이트)를 의미하고, 굵은 테두리의 직사각형은 하나의 블록을 나타낸다. 하얀 정사각형은 가용(free) 상태, 하늘색 정사각형은 할당(allocated) 상태를 의미한다. 진한 하늘색 정사각형은 패딩으로 할당된 상태를 의미한다.

위 그림에서 힙은 총 18개의 가용 블록이 어떻게 malloc 함수를 통해 할당되고, free 함수를 통해 해제되는지를 보여준다. 여기서 중요한 점은 malloc은 할당한 블록의 첫번째 블록을 가리키는 포인터를 반환한다는 것과(위 그림에서 p1, p2, p3, p4 포인터의 위치에 주목), 정렬을 맞추기 위해 패딩 데이터가 추가된다는 것이다. 위 그림의 (b)에서 malloc에는 (4*5 = )20바이트를 요청했지만 정렬을 맞추기 위해 추가 4바이트로 블록을 패딩한 것을 알 수 있다.
동적 메모리 할당이 필요한 이유
동적 메모리 할당이 필요한 이유는 이전 포스팅에서 자세하게 기록하였으므로 여기서는 간단하게만 정리해보자면, 결국 메모리를 낭비하지 않고, 수정하기 위해 재컴파일 하는 상황을 피하기 위해서이다.
할당기의 조건(Requirements)과 목표
명시적 할당기에는 아래의 엄격한 제약사항이 적용된다.
▪️ 임의의 요청 순서 처리 :
이전 할당 요청에 의해서 할당상태가 된 블록에 대해서만 해제 요청을 할 수 있다는 제약 사항만 잘 지킨다면 할당 요청과 해제(free) 요청은 무작위로 와도 상관이 없다. 따라서 할당기는 할당 요청이 언제 오고, 해제 요청이 언제 올지에 대해서 추측하지 않는다. 즉, 프로그래머가 신경써서 할당과 해제를 해야 한다!
▪️ 요청에 즉시 응답 :
할당기는 요청에 대해 즉시 응답하므로 요청받은 순서를 바꾸거나, 성능을 향상하기 위해 버퍼를 두지 않는다
▪️ heap 메모리 영역만 사용
▪️ 블록 정렬 :
할당기는 어떤 데이터 타입도 저장할 수 있도록 블록을 정렬해야 한다.
▪️ 할당된 블록을 수정하지 않음 :
할당기는 오로지 가용(free) 블록만을 수정할 수 있으므로, 일단 블록이 할당상태가 되고 나면 이를 옮기거나 수정하지 않는다.
할당기의 목표는 처리량(쓰루풋;throughput)과 메모리이용도(memory utilization) 사이의 최적의 지점을 찾는 것이다. 처리량의 정의는 단위시간당 처리가 완료되는 요청의 개수이다. 처리량을 최대화 하려면 요청을 처리하는 평균 시간을 최소화하면 된다. 처리량과 메모리 이용도를 동시에 올리기는 어렵기 때문에 둘 다 최대로 만들수는 없고 둘 사이의 최적의 지점을 찾아야 한다.
단편화 (Fragmentation)
단편화는 heap 메모리 이용도를 떨어뜨리는 주범으로서, 메모리가 가용상태임에도 불구하고 할당 요청을 처리하기 위해 사용될 수 없는 상황을 의미한다. 단편화에는 내부 단편화(internal fragmentation)와 외부 단편화(external fragmentation)가 존재한다.
내부 단편화는 필요한 데이터보다 더 큰 블록이 할당되었을 때 발생한다. e.g. 저장해야 하는 데이터는 1바이트인데 4바이트 블록이 할당
할당기가 부과하는 블록의 최소 사이즈가 할당 요청된 데이터(payload)의 크기보다 더 커서 발생하기도 하고, 할당기가 블록의 정렬을 맞추기 위해 (패딩으로) 블록의 크기를 증가 시켜서 발생할 수도 있다.

외부 단편화는 각각의 가용 블록들을 모두 합치면 필요한 데이터 이상이지만, 필요한 데이터 이상인 단일 블록이 없을 때 발생한다. 아래 그림에서 가용상태의 블록 (하얀 블록)은 모두 7개이지만, 6개 블록 할당 요청이 들어와도 어떠한 단일블록(이어진 블록)도 6보다 작기 때문에 이를 할당할 수 없다. 이러한 상황을 외부 단편화라고 한다.

외부 단편화는 앞으로 어떤 요청이 들어올지에 따라서 발생할 수도, 안할 수도 있다. 위의 상황에서 5개 블록 할당 요청과 2개 블록 할당요청이 순서대로 들어왔다면 아무런 외부 단편화 문제도 생기지 않았을 것이다. 이처럼 외부단편화의 발생 여부는 미래의 할당 요청에 따라 달려있기 때문에 수치화하고 예측하기가 어렵다. 이 때문에 대부분의 할당기들이 휴리스틱을 사용해서 많은 수의 자잘한 블록보다는 적은 수의 큰 블록들을 유지하려고 한다.
구현 이슈
직접 동적메모리할당기를 만들어본다고 하면 어떤 것들을 고려해야 할까? 동적메모리할당기의 목표 - 처리량과 메모리이용도 사이의 최적의 지점을 찾는다는 관점에서 아래의 사항들을 반드시 고려해야 해야 하고, 남은 포스팅에서는 아래의 각각의 사항들을 어떻게 처리하는지에 대해서 살펴 볼 것이다.
▪️ Free block organization : 가용 블록들을 찾아내서 할당해야 할텐데, 어떻게 가용블록을 구성(조직)해놓아야 할까?
▪️ Placement : 블록을 새로 할당할 때 가장 할당하기 적절한 위치를 어떻게 고를 것인가?
▪️ Spliting : 가용 블록의 일부를 할당한 후 남은 부분은 어떻게 분리할 것인가?
▪️ Coalescing : 새로 해제된 블록들을 기존의 가용 블럭들과 어떻게 연결시킬 것인가?
Free block organization - 묵시적 가용 리스트 (implicit free lists)
할당기는 할당된 블록과 가용 블록을 구별할 수 있는 블록의 경계가 필요하다. 그리고 대부분의 할당기들은 이런 경계가 될 수 있는 정보들을 블록 자체에 끼워넣는다. 블록 내에 저장해야 하는 정보(payload) 뿐 아니라 1 워드짜리(=4바이트) 헤더를 붙여서 블록의 크기와 할당 여부를 표시하고, 필요한 경우 정렬을 맞추기 위한 패딩도 포함한다. 아래의 그림으로 이러한 구조를 표현할 수 있다.

위 그림에서 빨간색 부분이 4바이트 크기의 헤더이다. 4바이트의 32비트 중 29비트는 블록의 사이즈를 표현하기 위해 사용되고 마지막 세바이트 중 가장 오른쪽 한 비트(그림에서 a로 표현된 부분)는 할당 유무를 나타낸다. 이 값이 1이면 할당이 된 상태, 0이면 가용 상태이다. 참고로 블록의 사이즈는 블록의 헤더, payload, 패딩 모든 것을 포함한 블록 전체 크기를 의미한다.
| 💡4바이트 헤더는 어떻게 사이즈와 할당 유무를 모두저장할 수 있는가 ? 블록은 항상 더블워드 정렬을 따른다. 이는 모든 블록 사이즈는 항상 8의 배수라는 것이고 2진수에서 8의 배수는 항상 끝 세 비트가 0이다. (십진수에서 10의 배수는 항상 마지막 숫자가 0이고, 100의 배수는 항상 마지막 두 숫자가 0이고, 1000의 배수는 항상 마지막 세 숫자가 0이라는 것을 생각해보면, 2진수에서 2의 배수는 마지막 숫자가 0이고 4의 배수는 마지막 두 숫자가 0이고 8의 배수는 마지막 세 숫자가 0이라는 것이 좀 더 와닿을 것이다. 블록 사이즈는 항상 8의 배수이기 때문에 마지막 세 비트는 원하는 대로 사용할 수 있다. 나중에 블록의 헤더로부터 사이즈를 알아내야 할 때 끝 세자리를 0으로 바꿔주는 연산을 수행하면 되기 때문이다. 따라서 4바이트 헤더에서는 32 비트 중 29비트를 주소를 표현하기 위해 사용하고 마지막 세 비트중 가장 오른쪽 비트 (the least significant bit)를 할당 유무를 표시하기 위해서 사용한다. 예를 들어 블록의 크기가 18이고 블록은 할당이 된 상태라고 해보자. 블록의 크기는 0x00000018 이고 할당여부는 0x1 일 것이다. 이 두 값에 대해 or연산을 하면 0x00000019가 된다. 이 값이 2진수로 헤더에 들어가는 값이 된다. 또 다른 예를 들어서 블록의 크기가 40이고 블록은 가용 상태라고 해보자. 블록의 크기는 0x00000028 이고 할당여부는 0x0 일 것이다. 이 두 값에 대해 or연산을 하면 0x00000028가 된다. 이 값이 2진수로 헤더에 들어가는 값이 된다. |
묵시적 가용리스트의 이름이 '묵시적' 가용리스트인 이유는 이렇게 헤더에 블록의 크기가 나와있기 때문에, 직접적으로(or 명시적으로) 다음 블록의 주소가 나와있지는 않더라도 (현재 주소 + 블록 크기)로 다음 블록의 시작점을 계산할 수 있기 때문이다. 아래 그림을 참고해보면 보다 이해가 쉽다. 그림에서 헤더의 n/m은 사이즈/할당유무 를 나타낸다. 위의 화살표를 보면 헤더를 통해서 다음 블록의 시작점으로 이동하며 순회(traverse)할 수 있다.

위 그림이 묵시적 가용 리스트의 구조이다. 가용 블록들은 마치 연결리스트와 같이 연결되어있고, 그 방법은 '묵시적'인 방법이다. 다음 블록을 가리키는 포인터가 블록 내에 직접 존재하는 것이 아닌, 블록의 사이즈를 통해서 계산해 나가는 간접적이고 묵시적인 방법이다. 그런데 위 구조에서 새로운 1워드 짜리 블록들이 보인다. 바로 힙의 맨 앞과 맨 끝에 있는 블록이다. 힙의 첫 블록은 사용되지 않는 블록으로 정렬을 맞추기 위해 필요하고, 맨 마지막 블록은 끝 블록이라는 것을 알려주기 위한 블록으로 크기는 0이고 할당된 상태를 가진 블록이다.
이렇게 묵시적 가용 리스트를 구성하면 간단하다는 장점이 있지만, 사용할만한 가용블록을 찾기 위해서 계속 순회하면서 가용리스트를 검색해야 하는 비용이 든다는 단점이 있다. 할당블록과 가용블록을 합쳐서 모두 N개의 블록이 있다고 하면 O(N)의 선형 시간이 든다.
시스템의 정렬 조건 (본 포스팅에서는 더블워드 정렬)과 묵시적 가용리스트의 블록 형식은 블록의 최소 사이즈를 결정한다. 저장할 데이터 (+ 필요하다면 패딩) 이외에도 최소한 4바이트 헤더는 가져야 한다는 것은 블록의 최소 사이즈는 8바이트라는 것이다. 만약 응용프로그램이 1바이트 할당만 요청하더라도 할당기는 8바이트, 즉 2-word 블록을 할당할 것이다.
Placing
응용프로그램이 k만큼의 바이트를 할당해달라고 요청하면 할당기는 k만큼을 할당할 수 있을만한 적절한 위치를 찾아본다. 적절한 할당 위치를 찾는 방법은 'placement policy'에 따라 결정되는데, 가장 일반적인 policies에는 first fit, next fit, best fit 방법이 있다.
first fit 방법은 리스트의 맨 처음부터 탐색을 시작해서 할당할 수 있는 (=크기가 k 이상이고 가용 상태인) 블록을 찾으면 더 이상 탐색을 진행하지 않는 방법이다. next fit 방법은 first fit과 유사하지만 리스트의 맨 처음부터 탐색을 하는 게 아닌, 이전의 검색에서 블록을 찾은 위치부터 검색을 시작하는 방법이다. best fit은 할당할 만한 블록을 찾았을 때 멈추지 않고 끝까지 탐색을 해서 모든 가용 블록을 검사한 다음 할당이 가능한 블록 중 가장 작은 블록을 찾는 방법이다.
간단하게 각 방법의 장단점을 확인해보자.
first fit 의 장점은 리스트의 뒷 부분에 있는 사이즈가 큰 가용 블록들을 사용하지 않고 유지하고 있을 가능성이 크다는 것이고, 단점은 리스트 앞쪽에 작은 가용 블록들 조각들이 남아있을 가능성이 크다는 것이다.
next fit의 장점은 이전에 가용 블록을 찾아낸 자리에서 부터 검색을 시작하기 때문에 더 빠르게 가용블록을 찾아낼 수 있다는 것이고 단점은 first fit에 비해 메모리 이용도가 떨어진다는 것이다
best fit 방법의 장점은 앞의 두 방법들에 비해 메모리 이용도가 높다는 것이고, 단점은 (당연하게도) 탐색에 시간이 오래걸린다는 것이다.
Splitting
할당기가 요청받은 만큼 할당할 위치를 찾고나면, 이제 얼마나 할당할 것인가를 결정해야 한다. 할당할 크기는 2word이고, 할당할 위치의 가용 블록은 8 word 짜리인데, 이 8 word 전체를 할당할 수는 없다. 남는 6-word 크기의 메모리는 내부 단편화를 유발한다. 메모리는 결국 유한한 자원이므로 남는 6word를 소중히 아껴써야 하기 때문이다.
즉 우리는 새로 할당할 가용 블록을 두 부분으로 나눠서, 첫 부분은 할당된 블록이 되고 남은 부분은 새로운 가용 블록이 되게 해야 한다. 아래 그림을 보자. 위의 메모리 그림의 가운데는 32/0 헤더를 가진 8-word 크기의 가용 블록이 있다. 할당기가 응용프로그램으로부터 3개 워드(12바이트)를 할당해달라는 요청을 받으면, 할당기는 헤더를 포함하여 4개 워드를 할당할 자리를 찾는다. 32/0 의 헤더를 가진 이 가용 블록에 4워드를 할당하면, 이 32/0 의 8워드 블록은 16/1 헤더를 가진 4워드 블록과 16/0 헤더를 가진 4워드 블록으로 나뉜다.

Coalescing Free Blocks
할당기가 할당된 블록을 해제 할때, 새로 해제된 블록의 좌우에는 다른 가용 블록들이 있을 수 있다. 아래 그림을 보자. p가 가리키는 4-word 크기의 블록을 해제했을 때 우측에도 2-word 크기의 가용 블록이 있다. 이렇게 4개짜리 가용 블록과 2개짜리 가용 블록이 붙어있는 상태에서 5-word를 할당하려고 할 때 할당할 수 있는 블록이 없다. 이를 false fragmentation, 가짜 단편화라고 한다. 분명 4개짜리와 2개짜리 가용블록을 붙이면 (연결하면; coalesce 하면) 6-word 짜리 가용 블록이 될 수 있음에도 이를 연결하지 않아 필요한 블록을 할당하지 못하는 문제가 생기는 것이다. 이러한 가짜 단편화를 해결하기 위해 할당기들은 coalescing이라고 불리는 방법으로 인접한 가용 블록들을 병합한다.

Coalescing with Boundary Tags
해제하려고 하는 블록을 '현재블록'이라고 할때, 현재블록의 다음 블록이 가용 블록인 경우는 간단하게 연결할 수 있다. 현재 블록을 해제 한 후 다음 블록의 헤더를 체크하여 할당 상태가 0이라면 (즉, 가용 블록이라면) 헤더에서 블록의 크기를 확인 한 후 현재 블록의 헤더에 이 크기를 더해준다. 아래 그림에서 기존의 헤더에서 블록 크기가 4였고, 인접한 다음 가용블록의 크기가 2 이므로, 현재 블록의 헤더에 블록크기를 4+2 = 6으로 업데이트해주면, 기존의 크기가 2였던 가용 블록은 '논리적으로' 사라지게 되는 것이다.

그런데, 현재 블록의 다음 블록이 아니라 이전 블록이 가용 블록인 경우에는 그리 간단하지 않다. 우선 왼쪽 블록이 가용블록인지 아닌지를 보고 판단할만한게 없다. 결국 가용 리스트를 처음부터 현재 블록을 만날 때까지 다 탐색하는 수 밖에 없다. 결국 블록을 해제하는데 선형 시간이 드는 것이다.
이를 해결하기 위해 'boundary tags' 라는 방법이 고안됐다. 블록의 맨 끝에 푸터(footer)를 붙이는 것이다. 이 footer가 바로 boundary tags 이다. 푸터의 내용은 헤더의 내용과 동일하게 블록의 크기 + 할당 정보이다. 헤더와 동일한 내용의 푸터를 블록 끝에 붙임으로서 할당기는 이전 블록이 시작하는 위치와 할당 상태를 알아낼 수 있게 된다.

현재블록을 해제하고 인접한 가용 블록과 연결하려 할 때, 4가지의 경우가 존재한다.

1. 현재 블록의 이전 블록, 다음 블록 모두 할당된 상태
2. 현재 블록의 이전 블록은 할당된 상태, 다음 블록은 가용상태
3. 현재 블록의 이전 블록은 가용 상태, 다음 블록은 할당된 상태
4. 현재 블록의 이전 블록, 다음 블록 모두 가용 상태
이제 블록은 boundary tag를 가지고 있다고 생각하고, 위의 네 가지 경우에서 어떻게 블록들이 연결 되는지를 살펴보자. 자료로 사용된 그림에서 a는 할당된 상태, f는 가용 상태를 나타낸다.
1. 현재 블록의 이전 블록, 다음 블록 모두 할당된 상태
인접한 블록들이 모두 할당된 상태이므로 연결이 수행되지 않는다. 현재 블록의 헤더와 푸터의 할당 여부를 표시하는 비트값만 바뀜으로서 논리적으로 블록이 할당 상태에서 가용 상태로 바뀐다.

2. 현재 블록의 이전 블록은 할당된 상태, 다음 블록은 가용상태
다음 블록이 가용 상태이므로 다음 블록과 연결한다. 현재 블록의 헤더가 그대로 연결된 블록의 헤더가 되고, 다음 블록의 푸터가 연결된 블록의 푸터가 된다. 이 헤더와 푸터의 값은 현재블록의 크기 + 다음 블록의 크기 값으로 바뀌고, 할당 상태도 0으로 바뀐다. 아래 그림에서 현재 블록의 크기가 n, 다음 블록의 크기가 m2 였으므로 연결된 새 가용블록의 크기는 n+m2 이다.

3. 현재 블록의 이전 블록은 가용 상태, 다음 블록은 할당된 상태
이전 블록이 가용 상태이므로 이전 블록과 연결한다. 이전 블록의 헤더가 그대로 연결된 블록의 헤더가 되고, 현재 블록의 푸터가 연결된 블록의 푸터가 된다. 이 헤더와 푸터의 값은 현재블록의 크기 + 이전 블록의 크기 값으로 바뀌고, 할당 상태도 0으로 바뀐다. 아래 그림에서 현재 블록의 크기가 n, 이전 블록의 크기가 m1 였으므로 연결된 새 가용블록의 크기는 n+m1 이다.

4. 현재 블록의 이전 블록, 다음 블록 모두 가용 상태
이전 블록과 다음 블록 모두 가용 상태이므로 이전 블록과 다음블록 모두 연결한다. 이전 블록의 헤더가 그대로 연결된 블록의 헤더가 되고, 다음 블록의 푸터가 연결된 블록의 푸터가 된다. 이 헤더와 푸터의 값은 현재블록의 크기 + 이전 블록의 크기 + 다음 블록의 크기 값으로 바뀌고, 할당 상태도 0으로 바뀐다 (이 경우 헤더와 푸터는 이미 가용 상태이므로 따로 할당상태를 바꿀 필요는 없다). 아래 그림에서 현재 블록의 크기가 n, 이전 블록의 크기가 m1, 다음 블록의 크기가 m2 였으므로 연결된 새 가용블록의 크기는 n+m1+m2 이다.
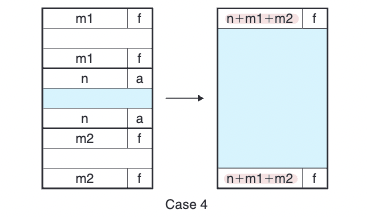
위의 과정을 살펴본 것과 같이 boundary 태그를 사용함으로서 블록을 해제하는 시간은 O(1)의 상수 시간로 매우 짧다. 하지만 boundary tag를 이용하는 방법에도 단점이 있는데, 블록에 헤더와 푸터를 모두 사용함으로서 데이터를 제외한 다른 부분들이 메모리에서 차지하는 양(=memory overhead)이 너무 커진다는 것이다. 작은 블록들이 여러 개 있는 경우에는 정도가 더 심하다. 이를 해결하는 여러 최적화 방법들이 존재하기는 하지만 이를 상세하게 다루지는 않겠다.
추가 heap 메모리가 필요할 때
블록을 할당할 수 있는 가용 블록이 아무것도 없다면. 할당기는 sbrk 함수를 호출함으로서 커널에 heap 메모리를 추가로 달라고 요청한다. 할당기가 추가로 메모리를 받으면 이를 하나의 가용 블록으로 변형하고 가용 리스트 안에 이 블록을 삽입한 다음 블록을 할당한다.
이제 지금까지 배운 내용들을 활용해서 직접 malloc 패키지 함수들을 구현해볼 수 있다.
이번 포스팅이 이미 너무 길어졌기 때문에 코드에 대한 내용 다음 포스팅에서 진행하도록 하겠다!
Reference
1. CMU malloc lab 강의 자료 (ppt)
2. Randal E. Bryant and David R. O'Hallaron, Computer Systems: A Programmer's Perspective, 3/E (CS:APP3e), Carnegie Mellon University, 2015
3. Randal E. Bryan , David R. O'Hallaron, 『컴퓨터 시스템』, 김형신 옮김, 피어슨에듀케이션코리아, 2016

댓글