자료구조의 기본 연산
자료구조의 네 가지 기본 연산 방법은 읽기, 검색, 삽입, 삭제 이다.
읽기: 특정 '위치'의 '값'을 찾아내는 연산 e.g. A배열의 3번째 값은 무엇인가?
검색: 특정 '값'의 '위치'를 찾아내는 연산 e.g. 'iphone'이라는 값이 A라는 배열에 존재하는가? 있다면 몇번째 위치에 존재하는가?
삽입: 새로운 값을 추가하는 연산 e.g. 'ipad'라는 값을 A라는 배열에 추가
삭제: 특정 인덱스의 값을 제거하는 연산 e.g. 'iMac'이라는 값을 A라는 배열에서 삭제
자료구조 연산의 속도 측정
자료구조를 배우는 궁극적인 목적은 가장 효율적인 자료구조를 사용하기 위해서이다.
그렇다면, 효율성이란 어떻게 측정될 수 있을까?
우선 '속도가 빠른' 자료구조가 효율적이라고 할 수 있으니 '속도'로 효율성을 측정할 수 있을 것이다.
연산의 속도 자체는 하드웨어에 따라서 다르다. 똑같은 자료구조의 읽기 연산을 하더라도, 내 macbook air보다 슈퍼컴퓨터의 연산속도가 훨씬 빠를 것이다. 따라서, 단순히 연산에 '몇 초'가 걸린다로 속도를 측정하기 보다는 '몇 단계'를 거치느냐를 기준으로 연산의 속도를 측정해야 한다. 그래서 연산의 속도 측정은 연산의 시간복잡도 측정이라고도 불린다.
💡 시간 복잡도는 최악의 시나리오(가장 많은 단계가 걸리는 경우)를 기준으로 판단한다.
각각의 연산에서 가장 연산이 오래걸리는 경우에 몇 단계가 필요한 지를 기준으로 속도를 측정하는 것이다.
그러면, 자료구조의 기본 연산 읽기, 검색, 삽입, 삭제의 속도, 즉 시간 복잡도는 어떨까? 각 연산은 몇 개의 계산 단계를 거치게 될 까? 우선 가장 기초적인 자료 구조 중 하나인 '배열'을 기준으로 각 연산의 시간복잡도를 살펴보고자 한다. (본 포스팅은 배열 기초에 대한 부분은 다루지 않으며, 배열 기초 지식이 있는 분들이 읽는 다는 가정 하에 쓰여졌다.)
배열의 읽기
읽기는 어떤 위치의 값이 무엇인지 찾아보는 것이다. 배열을 생성하고, 읽기를 해보았다.

javascript로 apple이라는 배열을 생성하고, apple[2]로 apple이라는 배열의 2번 인덱스를 읽자, iPad라는 값을 읽어왔다.
위와 같은 연산이 읽기 연산이다. 본론으로 돌아와서, 읽기 연산은 몇개의 단계를 거치게 될까?
컴퓨터는 메모리 주소까지 한번에 갈 수 있기 때문에 딱 한 단계면 읽기 연산을 끝낼 수 있다.
컴퓨터 메모리는 수많은 셀로 구성되어있고, 각 셀에는 순차적인 메모리 주소가 붙어있다. 컴퓨터는 배열을 저장할 때 이 배열이 어디서 시작하는 지를 함께 저장하기 때문에, 배열의 첫 원소(배열이 시작하는 지점)를 읽을 때는 한 번에 찾아낼 수 있고, 첫 원소가 아닌 원소를 읽을 때에도 메모리 주소에 인덱스 값을 더해서 가고자 하는 메모리 주소를 찾아 한 번에 이동한다.
위의 apple 배열의 원소과 인덱스, 메모리 주소들을 간단하게 그림으로 나타내면 아래와 같을 것이다.
| 원소 | "iMac" | "iPhone" | "iPad" |
| 인덱스 | 0 | 1 | 2 |
| 메모리 주소 | 1010 | 1011 | 1012 |
apple 배열이 저장될 때, 이 배열의 시작점이 1010라는 정보도 저장되어있으므로, apple[0] 과 같이 첫 원소를 읽을 때 컴퓨터는 바로 1010 메모리 주소의 값을 읽어온다. apple[2]와 같이 세 번째 원소를 읽는다면 컴퓨터는 배열의 첫 시작점 1010에다가 인덱스 2를 더해 1012라는 메모리 주소를 찾아 해당 값을 읽어온다.
이와 같이 배열의 읽기 연산은 한 단계로 끝나는 아주 빠른, 즉 아주 효율적인 연산이라는 것을 알 수 있다.
배열의 갯수가 1개여도, 10개여도, 100개여도, N개여도 항상 한 단계로 끝낼 수 있다.
배열의 검색
검색은 특정 값이 배열의 몇번째 인덱스에 있는지 (또는 없는지) 찾아보는 것이다.
컴퓨터는 모든 메모리 주소에 한 단계로 접근할 수 있지만, 각 메모리 주소에 어떤 값이 있는 지는 까보기(?) 전까지 바로 알지 못한다. 아파트 1401호는 14층 왼쪽 호수에 있다는 걸 알기에 엘레베이터로 14층으로 바로 이동할 수 있지만, '홍길동'이라는 사람이 어디에 사는 지는 각 호수의 문을 두드려보고 안에 누가 있는지 확인해봐야 할 수 있는 것과 같다. (쓰고보니 비유가 별로군?)
위의 apple 배열을 가지고 얘기해보자면, apple 배열에서 "iPhone"이라는 값은 몇번째 인덱스에 존재하는지를 찾아보는 것이 검색이다.

위와 같이 iPhone이 apple 배열의 몇 번째 인덱스 인지를 검색해보았을 때, 컴퓨터는 0번째 인덱스부터 'iPhone'이라는 값을 찾아본다. 0에는 "iMac"이 있기 때문에 인덱스 1을 확인한다. 인덱스 1의 값은 찾고 있던 값 "iPhone"이므로 더이상 검색을 수행하지 않는다. 참고로 이러한 방식, 한 번에 한 셀씩 확인하는 방법을 '선형검색 (linear search)' 라고 부른다.
위의 경우에는 두 단계가 걸렸다. iPhone이 인덱스1에 있었기에 두 단계로 끝났지, 만약 맨 끝에 있었다면? 아니면 이 배열에 존재하지 않았다면? 배열의 모든 원소를 다 확인해봤어야 했기에 세 단계가 걸렸을 것이다. 배열의 원소가 100개 였다면, 100번을 확인해야 하고, 배열의 원소가 1000개 였다면 1000번을 확인해야 한다.
즉, 원소의 개수가 N개일 때 배열의 검색에서 최악의 시나리오는 N 단계가 걸리는 경우이다.
배열의 삽입
삽입은 배열에 새 데이터를 추가하는 연산이다. 계속해서 apple 배열을 사용하여 "appleWatch" 데이터를 추가해보려고 한다.

데이터를 배열의 맨 끝에 삽입한다면, 배열을 찾아서 데이터를 삽입하기만 하면 되므로 한 큐에 끝난다.
하지만 맨 앞이나, 중간에 삽입하려고 한다면, 데이터를 추가하는 위치 이후의 모든 원소를 뒤로 옮기는 단계가 추가된다. 인덱스 0번 자리 (맨 앞)에 추가한다면 iMac, iPhone, iPad를 모두 한 칸씩 뒤로 순차적으로 옮겨야 하므로 세 단계가 추가된다. 만약 인덱스 2번 자리에 추가한다면, iPad를 한 칸씩 뒤로 옮겨야 하므로 한 단계가 추가된다. 추가하는 자리 뒤로 원소가 100개 였다면, 100번을 옮겨야 하고, 배열의 원소가 1000개 였다면 1000번을 옮겨야 한다.
즉, 원소가 N개인 배열의 삽입에서 최악의 시나리오는 배열의 맨 앞에 데이터를 추가하는 경우이고, 이 때 N+ 1 단계가 걸린다. (데이터 옮기 N 단계 + 데이터 삽입하기 1 단계)
배열의 삭제
배열의 삭제는 특정 인덱스의 값을 제거하는 것이다. apple 예제에서 1번 인덱스의 값을 제거해보았다.
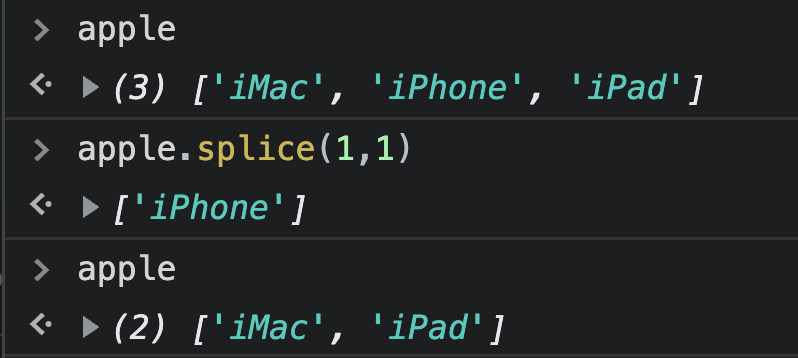
배열을 삭제할 때는 특정 인덱스을 찾아 삭제하는 단계와, 삭제된 빈 공간을 메꾸기 위해 이후의 모든 원소를 앞으로 하나씩 이동하는 단계가 필요하다. 맨 마지막 원소를 삭제하는 경우에는 이동이 필요하지 않겠지만, 앞이나 중간의 원소를 사용하면 이동이 필요하다.
배열의 맨 앞 원소를 삭제하는 경우에는, 삭제된 원소를 제외한 나머지 모든 원소를 다 이동해야 하므로 가장 많은 단계가 필요하다. 즉, 최악의 시나리오의 경우 특정 인덱스 값을 삭제하고 (1단계) N-1개의 원소를 이동해야 하므로(N-1단계) 총 N 단계가 필요하다.
정리해보자면 배열에서 기본 연산 읽기, 검색, 삽입, 삭제는 원소의 개수가 N개일 때 아래와 같은 단계가 필요하다.
| 연산 종류 | 배열의 읽기 | 배열의 검색 | 배열의 삽입 | 배열의 삭제 |
| 단계 (시간복잡도) | 1 | N | N+1 | N |
위의 단계는 '배열' 에만 해당하는 것으로 배열이 아닌 다른 자료 구조를 사용할 때는 필요한 단계가 달라진다.
집합의 기본 연산
가령 집합('배열 기반 집합'에 한정)이라는 자료구조의 경우, 배열과 유사하지만 중복 값을 허용하지 않는 다는 차이점이 있는 자료 구조이다. 중복 값을 허용하지 않는다는 이 특징 하나가 연산의 단계에는 큰 차이점을 불러온다.
집합의 읽기, 검색, 삭제 연산에서 필요한 단계는 배열에서와 동일하다. 단, 삽입 연산의 경우 더 많은 단계가 필요하다.
배열에서는 삽입의 경우 삽입+원소의 이동 단계가 필요했지만, 집합에서 삽입의 경우 삽입하려는 값이 이미 존재하지는 않는지 모든 데이터를 검색하는 단계가 추가로 필요하기 때문이다. 즉 최악의 시나리오에서 원소가 N개인 집합의 삽입에는 배열의 삽입에 필요한 N+1 외에도 모든 데이터를 검색하는 N단계가 필요하여 2N+1 단계가 필요하다.
즉 집합과 배열의 시간 복잡도를 비교하자면 아래와 같다.
| 자료 구조 | 읽기 | 검색 | 삽입 | 삭제 |
| 배열 | 1 | N | N+1 | N |
| 집합 | 1 | N | 2N+1 | N |
이를 통해 생각해봐야 할 것은 요구사항에 맞는 가장 효율적인 자료구조를 사용해야 한다는 것이다. 중복을 불허하는 요구사항이 있는 경우에는 효율성이 낮더라도 집합을 사용해야 할 것이고, 중복을 허용하는 경우에는 배열을 사용하는 것이 당연지사 효율적이다.
이처럼 각 자료구조에서의 연산들이 어떤 시간복잡도를 갖고 있는지를 토대로 가장 효율적인 자료구조를 고를 수 있어야 한다.
다음 포스팅에서는 새로운 자료구조인 '정렬된 배열'과 함께 알고리즘에 대해서 정리해보겠다.
참고문헌: 제이 웬그로우, 『누구나 자료구조와 알고리즘』, 심지현, 길벗, 2011
누구나 자료 구조와 알고리즘 - YES24
사칙 연산으로 복잡한 알고리즘을 쉽게 이해해보자수학 용어와 전문 용어가 아니어도 이해한다이 분야의 책은 대부분 컴퓨터 공학 전공자를 대상으로 쓰였거나 고등학교 수학을 잘 안다고 가
www.yes24.com
'자료구조 & 알고리즘' 카테고리의 다른 글
| [📚누구나 자료구조와 알고리즘] 12-1. 동적 프로그래밍 - 불필요한 재귀 호출 줄이기 (0) | 2022.10.14 |
|---|---|
| [📚누구나 자료구조와 알고리즘] 3. Big-O Notation : O(N), O(1), O(logN), O(N^2) (1) | 2022.09.13 |
| [📚누구나 자료구조와 알고리즘] 2. 알고리즘이 중요한 까닭 - 선형검색과 이진검색 (0) | 2022.09.08 |




댓글